Eine Tangente (lat., wörtl. „Berührende“) ist in der Geometrie eine Gerade, die eine Kurve berührt, also einen gemeinsamen Punkt mit ihr hat, ohne dass sie die Kurve schneiden würde.
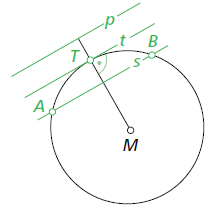
Am Kreis unterscheidet man zwischen Tangente, Sekante und Passante: Eine Tangente hat genau einen gemeinsamen Punkt (T) mit der Kreislinie, eine Sekante zwei (A und B) und eine Passante überhaupt keinen.
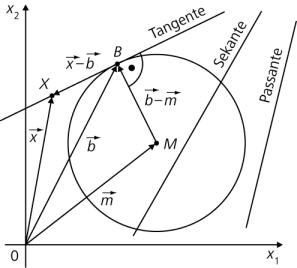
In der Analytischen Geometrie werden Tangenten wie alle Geraden durch Gleichungen angegeben. Für eine Tangente, die einen Kreis k mit Mittelpunkt M(m1|m2) und Radius r im Punkt B(b1|b2) berührt, gibt es die folgenden möglichen Gleichungen:
- \((\vec b - \vec m) \circ (\vec x - \vec b) = 0\)
- \((\vec b - \vec m) \circ (\vec x - \vec m) = r^2\)
Dabei bezeichnet „\(\circ\)“ das Skalarprodukt zwischen den jeweilgen Differenzenvektoren.
In der Analysis untersucht man Tangenten an Funktionsgraphen.