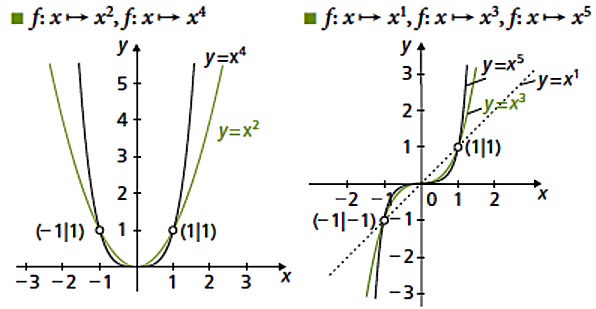Funktionsgraphen können, wie jedes geometrische Objekt, grundsätzlich ganz verschiedene Symmetrien aufweisen. Bei einer Kurvendiskussion interessiert man sich aber vor allem für die folgenden beiden Symmetrien:
- Punktsymmetrie zum Ursprung. Dies ist genau dann der Fall, wenn im ganzen Definitionsbereich D, also für alle \(x \in D\) gilt:
f(–x) = –f(x) - Achsensymmetrie zur y-Achse. Dies liegt genau dann vor, wenn für alle \(x \in D\) gilt:
f(–x) = f(x) - Ein einzelner Funktionsgraph kann nicht symmetrisch zur x-Achse sein, weil es zu jedem x nur höchstens einen Funktionswert geben darf. Zwei Funktionsgraphen f und g mit Df = Dg = D können jedoch zueinander spiegelsymmetrisch bezüglich der x-Achse sein. Dies ist genau dann der Fall, wenn für alle \(x \in D\) gilt, dass f(x) = –g(x).
Beispiele:
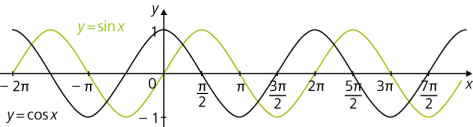
Der Graph der Sinusfunktion (grün) ist punktsymmetrisch zum Urpsrung, der Graph der Kosinusfunktion (schwarz) ist (achsen)symmetrisch zur y-Achse.
Alle Potenzfunktionen mit geradem Exponent sind (achsen)symmetrisch zur y-Achse, der Graph einer Potenzfunktion mit ungeradem Exponent ist punktsymmetrisch zum Urpsrung.
Aus diesem Grund nennt man auch Funktionen, die achsensymmetrisch zur y-Achse sind und für die somit f(–x) = f(x) im gesamten Definitionsbereich erfüllt ist, gerade Funktionen.
Entsprechend heißen Funktionen, die punktsymmetrisch zum Ursprung sind und für die somit f(–x) = –f(x) im gesamten Definitionsbereich erfüllt ist, ungerade Funktionen.
Achtung: Die meisten Funktionen sind weder gerade noch ungerade!
Allgemeine Symmetrie
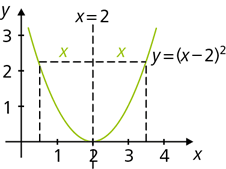
Der Graph einer Funktion f ist achsensymmetisch zur vertikalen Geraden x = a, wenn für alle \(x \in D_f\) gilt: f(a – x) = f(a + x).
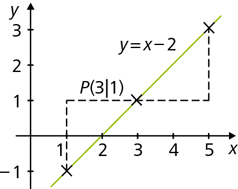
Der Graph einer Funktion f ist punktsymmetrisch bezüglich des Punkts P(a|b), wenn für alle \(x \in D_f\) gilt: b – f(a – x) = f(a + x) – b.
Beispiele:
- \(f:x\mapsto (x-2)^2, \ x \in \mathbb{R}\).
- \(f:x\mapsto x-2, \ x \in \mathbb{R}\)
Außer Punkt- und Achsenspiegelungen kann man auch Verschiebungen, Streckungen oder Stauchungen von Funktionsgraphen durch einfache „Manipulationen“ am Funktionsterm untersuchen.