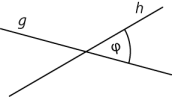
Unter dem Schnittwinkel \(\varphi\) zwischen zwei verschiedenen Geraden g und h versteht man den nicht stumpfen Winkel an der Geradenkreuzung.
Dabei bezeichnet „\(\circ\)“ das Skalarprodukt zwischen den beiden Richtungsvektoren \(\vec u\) und \(\vec v\).
Beispiel:
\(\displaystyle g : \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} -2 \\ 7 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}, \quad \lambda \in \mathbb R\)
\(\displaystyle h: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} -6 \\ 4 \\ -1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} , \quad \mu \in \mathbb{R}\)
\(\displaystyle \cos \varphi = \frac{\left|\begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}\circ \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}\right|}{\sqrt{3^2+2^2+1^2} \cdot \sqrt{1^2+1^2+2^2}} = \frac{|3 \cdot 1 + 2 \cdot 1 + 1 \cdot 2|}{\sqrt{14} \cdot \sqrt{6}} = \frac{7}{\sqrt{84}}\)
\(\displaystyle \Rightarrow \varphi = \cos^{-1}\frac{7}{\sqrt{84}}\approx 40^{\circ}\)