Unter einer Nullstelle versteht man bei einer Funktion f einen x-Wert \(x_0 \in D_f\), dessen Funktionswert f(x0) = 0 ist. Der Punkt (0|x0) ist damit ein Schnitt- oder Berührpunkt des Funktionsgraphen von f mit der x-Achse.
Man findet die Nullstellen einer Funktion durch Lösen der Gleichung f(x0) = 0. Dabei kann es, etwa bei rationalen oder Potenzfunktionen, dazu kommen, dass eine bestimmte Stelle mehrfach als Lösung ermittelt wird. Beispielsweise ist bei der Normalparabel y = x2 der Ursprung einer sog. doppelte Nullstelle. Allgemein gilt:
Wenn ein x-Wert eine doppelte, vierfache, sechsfache usw. Nullstelle ist, hat der Funktionsgraph dort einen Berührpunkt mit der x-Achse, bei einer einfachen, dreifachen, fünffachen usw. Nullstelle schneidet sie die Achse.
Beispiel:
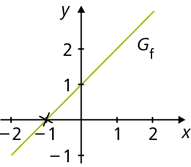
\(f:x \mapsto x+1 \ \ (x \in \mathbb R)\)
\(f(x)=0 \Leftrightarrow x+1=0\Leftrightarrow x=-1\)
f besitzt also die (einfache) Nullstelle: x = –1. Der Graph Gf schneidet die x-Achse in (–1|0).
In der Differenzialrechnung betrachtet man auch die Nullstellen der Ableitungen einer Funktion: Nullstellen der 1. Ableitung können Extremstellen sein, Nullstellen der 2. Ableitung Wendestellen.