-
Aufgabe 1
Dauer: 10 Minuten 8 PunkteIn einem rechtwinkligen Dreieck ABC ist die Hypotenuse c 12 cm lang und der Hypotenusenabschnitt q ist 8 cm lang.
- Fertige eine Skizze an!
- Berechne die Länge der Katheten, die Länge des anderen Hypotenusenabschnittes, die Höhe, Flächeninhalt des Dreiecks.
-
Aufgabe 2
Dauer: 7 Minuten 3 PunkteBerechne die Länge der horizontalen Diagonale \(d\).
-
Aufgabe 3
Dauer: 6 Minuten 6 PunkteIn einem gleichschenkligen Dreieck mit den Schenkeln a und der Grundseite c beträgt der Flächeninhalt 54 cm2. Die Grundseite c hat eine Länge von 6 cm.
- Welche Länge hat die Höhe hc?
- Welche Länge haben die Schenkel a?
-
Aufgabe 4
Dauer: 5 Minuten 4 PunktePrüfe, ob das Dreieck ABC einen rechten Winkel hat.
- a = 12 cm, b = 5 cm, c = 13 cm
- a = 6 cm, b = 12 cm, c = 7 cm
-
Aufgabe 5
Dauer: 9 Minuten 4 PunkteEin Zelt hat die Form einer Pyramide mit quadratischer Grundfläche. Das Zelt ist 1,80 m hoch. Von der Spitze des Zeltes verläuft ein Reißverschluss zum Mittelpunkt einer Grundseite. Der Reißverschluss ist 2,20 m lang.
- Fertige eine Skizze an und trage die gegebenen Längen ein.
- Welche Grundfläche hat das Zelt?
-
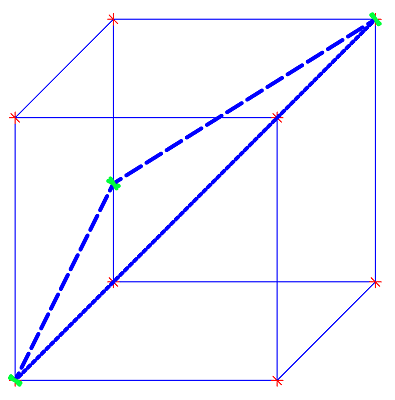
Aufgabe 6
Dauer: 8 Minuten 6 PunkteZwei Käfer haben sich in ein Wohnzimmer verirrt. Das Zimmer ist würfelförmig mit der Seitenkante s. Der eine Käfer krabbelt auf direktem Weg von der vorderen, unteren Ecke die Wände entlang zur oberen, hinteren Ecke (siehe Skizze). Der andere Käfer fliegt auf direktem Weg entlang der Raumdiagonale.
- Berechne die Länge der Krabbelstrecke sowie die Länge der Flugstrecke in Abhängigkeit von s.
- Um wie viel Prozent ist die Krabbelstrecke länger als die Flugstrecke?
-
Aufgabe 1
In einem rechtwinkligen Dreieck ABC ist die Hypotenuse c 12 cm lang und der Hypotenusenabschnitt q ist 8 cm lang.
- Fertige eine Skizze an!
- Berechne die Länge der Katheten, die Länge des anderen Hypotenusenabschnittes, die Höhe, Flächeninhalt des Dreiecks.