-
Aufgabe 1
Dauer: 10 Minuten 8 PunkteBestimme die maximalen Intervalle, in denen der Graph von f streng monoton steigt.
\(f(x)=x^3-3x+2\)
-
Aufgabe 2
Dauer: 8 Minuten 4 PunkteBegründe, ob die Funktion gerade, ungerade oder weder gerade noch ungerade ist.
-
\(f(x)=x^5-2x\)
-
\(f(x)=2x^4+x^3\)
-
\(f(x)=\frac{x^3\ -\ x}{x^2\ +\ 1}\)
-
\(f(x)=\frac{x^5\ -\ 3x}{2x^3\ +\ x}\)
-
Aufgabe 3
Dauer: 6 Minuten 3 PunkteGib den Term einer Funktion an, die folgende Eigenschaften besitzt: Ihr Graph ist achsensymmetrisch zur y-Achse und für \(x<0\) streng monoton steigend.
Des Weiteren gilt: \(\lim\limits_ {x \rightarrow \infty}f(x)=-2\).Skizziere auch den Graphen der Funktion.
-
Aufgabe 4
Dauer: 11 Minuten 7 PunkteGib die kleinstmögliche natürliche Zahl n an, sodass die Grenzwerte stimmen.
-
\(\lim\limits_ {x \rightarrow \ - \infty}x^n+2x^2-1=-\infty\)
\(\lim\limits_ {x \rightarrow \ \infty}x^n+2x^2-1=\infty\)
-
\(\lim\limits_ {x \rightarrow \ - \infty}-0,5x^n-1=-\infty\)
\(\lim\limits_ {x \rightarrow \ \infty}-0,5x^n-1=-\infty\)
-
\(\lim\limits_ {x \rightarrow \ \infty}n^x=1\)
-
\(\lim\limits_ {x \rightarrow \ \infty}\frac{1}{x^n}-1=-1\)
-
\(\lim\limits_ {x \rightarrow \ \infty}\frac{x^4\ +\ 2x}{x^n\ -\ 7}=0\)
-
\(\lim\limits_ {x \rightarrow \ \infty}\frac{x^3\ +\ 2x}{2x^n\ -\ 5x}=0,5\)
-
\(\lim\limits_ {x \rightarrow \ \infty}\frac{x^n\ +\ 5x\ +\ 1}{2x^3\ +\ x^2\ -\ 3}=\infty\)
-
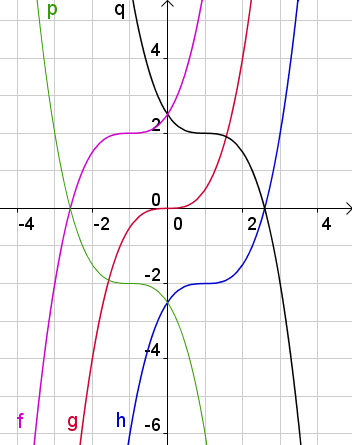
Aufgabe 5
Dauer: 10 Minuten 8 PunkteGib an, welcher Graph zu welcher Gleichung gehört.
-
\(y=0,5x^3\)
-
\(y=0,5(x-1)^3-2\)
-
\(y=-0,5(x-1)^3+2\)
-
\(y=0,5(x+1)^3+2\)
-
\(y=-0,5(x+1)^3-2\)
Beschreibe, wie man aus den Graphen den folgenden erhält: B aus A, C aus B, D aus C und E aus D.
-
Aufgabe 1
Bestimme die maximalen Intervalle, in denen der Graph von f streng monoton steigt.
\(f(x)=x^3-3x+2\)