-
Aufgabe 1
Gegeben ist die Funktion \(f\) mit \(f(x)=\frac{1}{x+1}-\frac{1}{x+3}\) und Definitionsbereich \(D_f=\mathbb{R}\backslash \{-3;-1\}\). Der Graph von \(f\) wird mit \(G_f\) bezeichnet.
a) Zeigen Sie, dass \(f(x)\) zu jedem der drei folgenden Terme äquivalent ist:
\(\frac{2}{(x+1)(x+3)};\ \frac{2}{x^2+4x+3};\ \frac{1}{0,5\cdot(x+2)^2-0,5}\)
b) Begründen Sie, dass die \(x\) - Achse horizontale Asymptote von \(G_f\) ist, und geben Sie die Gleichungen der vertikalen Asymptoten von \(G_f \) an. Bestimmen Sie die Koordinaten des Schnittpunkts von \(G_f\) an. Bestimmen Sie die Koordinaten des Schnittpunkts von \(G_f \) mit der \(y\)- Achse.
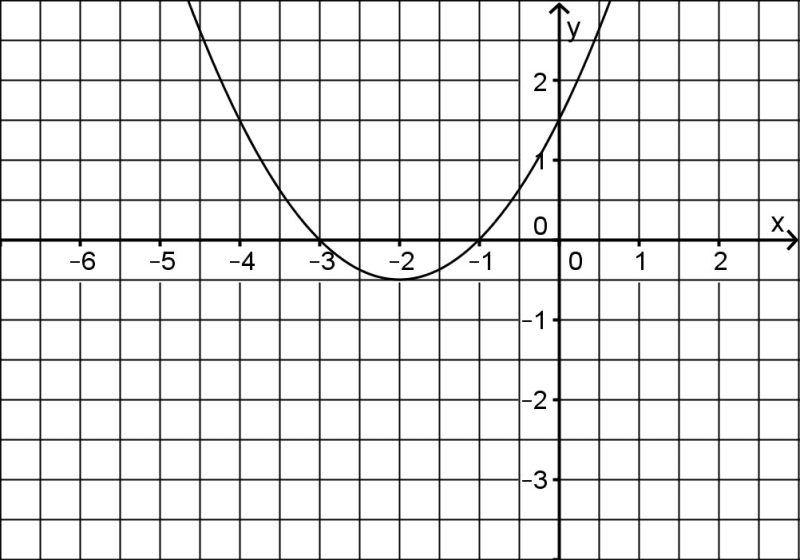
Abbildung 1 zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(p: x\mapsto 0,5\cdot (x+2)^2-0,5\), die die Nullstellen \(x=-3\) und \(x=-1\)hat. Für \(x \in D_f\) gilt \(f(x)= \frac 1{p(x)}\).
c) Gemäß der Quotientenregel gilt für die Ableitungen \(f'\) und \(p'\) die Beziehung \(f'(x)=-\frac{p'(x)}{(p(x))^2}\) für \(x \in D_f\).
Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von \(f'(x)\) und \(p'(x)\), dass \(x=-2\) einzige Nullstelle von \(f'\) ist und dass \(G_f\) in \(]-3;-2[\) streng monoton steigend sowie in \(]-2;-1[\) streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von \(G_f\) an.
d) Berechnen Sie \(f(-5)\) und \(f(-1,5)\) und skizzieren Sie \(G_f\) unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1.
Abiturprüfung
Mathematik
Abitur