Mathematik
5. Klasse
‐
Abitur
Mittlere Steigung von Funktionsgraphen
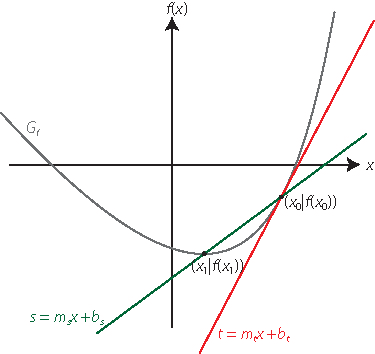
Die mittlere Steigung (oder Änderungsrate) eines Funktionsgraphen Intervall x 1 ; x 0 ] ist die Steigung der Sekante, welche den Graphen in den Punkten (x 1 |f (x 1 )) und ( x 0 | f ( x 0 )) schneidet. Dagegen entspricht die momentane Änderungsrate an der Stelle x 0 der Tangentensteigung in diesem Punkt und damit der ersten Ableitung \(f'(x_0)\) an dieser Stelle.
Zugehörige Videos und Aufgaben
Registriere dich kostenlos und nutze für 2 Tage die PremiumPlus Flat mit allen Funktionen
Übungen, Klassenarbeiten und mehr testen
Jetzt 2 Tage testen
Zugehörige Klassenarbeiten
Die Funktion \(f\) ist gegeben durch \(f(x) =(2-x)\cdot e^x\) , \(x\in \mathbb {R}\) . Die Graphen der Funktion \(f\) und ihrer Ableitungsfunktion \(f'\) sind in der Abbildung dargestellt. Die Lösungsvorschläge liegen nicht in der Verantwortung des jeweiligen Kultusministeriums.
Ein Ölfeld wird seit Beginn des Jahres 1990 mit Bohrungen in mehreren Erdöl führenden Schichten erschlossen. Die momentane Förderrate 1 aus diesem Ölfeld im Zeitraum von Anfang 1990 bis Ende 2009 kann im Intervall \( [0;20]\) durch die Funktion \(f\) mit der Gleichung \(f(t)=(1020-40t) \cdot e^{0,1 \cdot t};\quad t \in \mathbb R\) modelliert werden. Dabei wird \(t\) als Maßzahl zur Einheit 1 Jahr und \( f(t)\) als Maßzahl zur Einheit 1000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt \( t=0\) entspricht dem Beginn des Jahres 1990. Der Graph von \(f\) ist in der Abbildung 1 in dem für die
In ein Staubecken oberhalb eines Bergdorfes fließt ein Bach. Die momentane Zuflussrate 1 aus dem Bach kann an einem Tag mit starken Regenfällen durch die Funktion \(f\) mit der Gleichung \(f(t) = \frac14 t^3 -12t^2 +144t +250;\quad t \in \mathbb{R}\) , für einen bestimmten Beobachtungszeitraum modelliert werden. Dabei fasst man \(t\) als Maßzahl zur Einheit \(1\,\text{h}\) und \(f(t)\) als Maßzahl zur Einheit \(1\,\frac{\text{m}^3}{\text{h}}\) auf. Der Beobachtungszeitraum beginnt zum Zeitpunkt \(t = 0\) und endet zum Zeitpunkt \(t = 24\) . Die Lösungsvorschläge liegen nicht in der
In ein Staubecken oberhalb eines Bergdorfes fließen zwei Bäche. Nach Regenfällen unterschiedlicher Dauer und Stärke können die momentanen Zuflussraten 1 aus den beiden Bächen durch Funktionen \( f_a\) für den Bach 1 und \( g_a \) für den Bach 2 und die Gesamtzuflussrate aus den beiden Bächen durch eine Funktion \(h_a \) für einen bestimmten Beobachtungszeitraum modelliert werden. Gegeben sind für \(a>0\) zunächst die Funktionsgleichungen: \(f_a(t) = \frac 1 4 t^3 - 3a \cdot t^2 + 9a^2 + 340;\quad t \in \mathbb R\) \(h_a(t) = \frac 1 4 t^3 - 7a \cdot t^2 + 24a^2 + 740;\quad t \in \mathbb R