-
Aufgabe 1
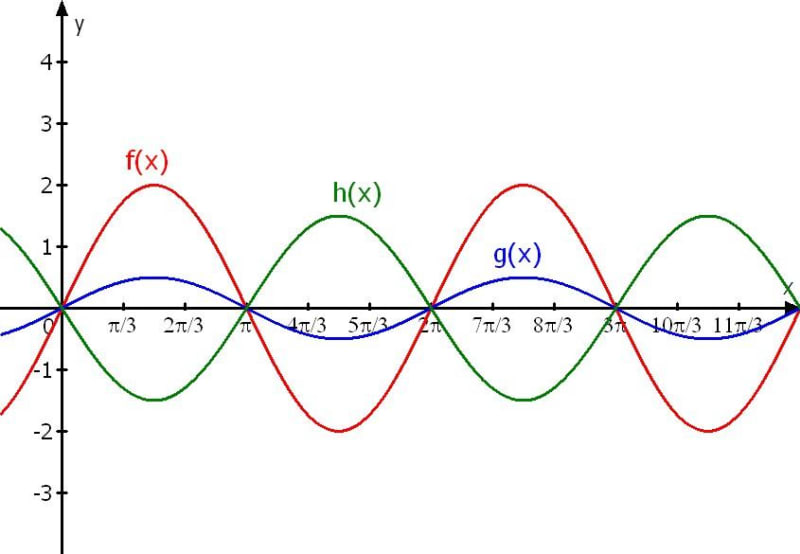
Dauer: 5 Minuten 5 PunkteBestimme zu den abgebildeten Graphen den Funktionsterm in der Form \(f(x)=a\cdot\sin(x)\).
-
Aufgabe 2
Dauer: 5 Minuten 5 PunkteBestimme zu den abgebildeten Graphen den Funktionsterm in der Form \(f(x)=\sin(b\cdot x)\).
-
Aufgabe 3
Dauer: 6 Minuten 3 PunkteBestimme den Wertebereich (die Amplitude), die Periode und die Nullstellen der Funktion \(f(x)=3\cdot \cos(2\cdot x).\)
-
Aufgabe 4
Dauer: 10 Minuten 5 PunkteSkizziere den Graphen der Funktion \(f(x)=\cos(3x)\) im Intervall \(0\leq x\leq 2\pi\) in dem Koordinatensystem unten. Bestimme die Nullstellen und die Periode der Funktion.
-
Aufgabe 5
Dauer: 6 Minuten 6 PunkteBestimme die erste Ableitung zu den folgenden Funktionen:
- \(f(x)=2-\sin(x)\)
- \(g(x)=\cos(x)-3\cdot \sin(x)\)
- \(h(x)=2\cdot x^3+cos( x)\)
-
Aufgabe 6
Dauer: 13 Minuten 5 PunkteBestimme den Schnittpunkt S der Graphen von \(f(x)=\sin(x)\) und \(g(x)=\cos(x)\) im Bereich \(0\leq x\leq \frac{\pi}{2}.\)Bestimme anschließend den Schnittwinkel im Punkt S, unter dem sich die Graphen von \(f \) und \(g\) schneiden.
-
Aufgabe 1
Bestimme zu den abgebildeten Graphen den Funktionsterm in der Form \(f(x)=a\cdot\sin(x)\).