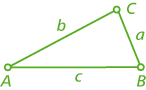
Ein Dreieck ist bestimmt durch drei Punkte A, B und C, die nicht auf einer Geraden liegen. Sie heißen Eckpunkte oder Ecken. Dabei werden die Ecken wie bei allen Polygonen (Vielecken) immer gegen den Uhrzeigersinn (im mathematisch positiven Drehsinn) nummeriert!
Die Seiten sind die Strecken zwischen jeweils zwei Ecken
Die Seiten werden durch je zwei Eckpunkte bestimmt. Sie werden jeweils mit dem Kleinbuchstaben bezeichnet, der dem gegenüberliegenden Eckpunkt entspricht, d. h. a, b bzw. c (siehe Bild oben).
Die Innenwinkel liegen im Innern des Dreiecks und werden von je zwei Seiten eingeschlossen. Man bezeichnet sie mit \(\alpha , \beta , \gamma\) . Die Außenwinkel liegen außerhalb des Dreiecks und werden von einer Seite und der Verlängerung einer anderen eingeschlossen. Man bezeichnet sie mit \(\alpha _1, \alpha _2, \beta _1, \beta _2, \gamma _1, \gamma _2\) (siehe Bild).
Wenn alle drei Winkel kleiner als 90° sind, heißt das Dreieck spitzwinklig, ist einer größer als 90°, heißt es stumpfwinklig. Beträgt ein Winkel genau 90°, ist das Dreieck rechtwinklig (siehe unten). Nach dem Winkelsummensatz beträgt die Summe aller drei Winkel immer genau 180°, also kann nie mehr als ein Winkel recht- oder stumpfwinklig sein.
Gleichen Winkeln liegen immer gleiche Seiten gegenüber, dem kleinsten Winkel liegt die kürzeste Seite gegenüber.
Der Flächeninhalt A eines Dreiecks ist das halbe Produkt aus einer Seite und der dazugehörigen Höhe: \(\displaystyle A = \frac{1}{2}\cdot a\cdot h_a = \frac{1}{2}\cdot b\cdot h_b = \frac{1}{2}\cdot c\cdot h_c\) (vergleiche die Flächenberechnung beim Parallelogramm). In der Analytischen Geometrie kann man diesen Flächeninhalt auch mithilfe des Kreuzprodukts der Verbindungsvektoren zwischen den Eckpunkten berechnen:
\(\displaystyle A = \frac{1}{2} \cdot \left| \overrightarrow{AB} \times \overrightarrow{AC} \right| = \frac{1}{2} \cdot \left| \overrightarrow{AB} \right| \cdot \left| \overrightarrow{AC} \right| \cdot \sin \alpha\)
Bestimmte Dreiecke weisen besondere Symmetrien auf und sind daher leichter zu untersuchen, inbesondere gleichschenklig, gleichseitig und rechtwinklige Dreiecke.
Im Dreieck werden auch bestimmte Linien speziell ausgezeichnet und als „besondere Linien“ bezeichnet, sie treten immer zu dritt auf (eine pro Seite/Ecke), z. B. drei Höhen, drei Seitenhalbierende usw. In einem gleichseitigen Dreieck fallen für eine gegebene Seite bzw. Ecke alle besonderen Linien zusammen.
Eine wichtige Aufgabe ist die Konstruktion von Dreiecken mit Zirkel und Lineal, wenn bestimmte „Hauptstücke“ (z. B. drei Seiten oder zwei Winkel und die eingeschlossene Seite) gegeben sind. Wann dies eindeutig möglich ist, geben die Kongruenzsätze für das Dreieck an. Die Ähnlichkeitssätze geben an, wann zwei Dreieck die gleiche Form haben (aber möglicherweise unterschiedlich groß sind).
Ab der neunten oder zehnten Klasse spielt die Trigonometrie eine wichtige Rolle bei der Untersuchung von Dreiecken. Mit den Winkelfunktionen kann man einerseits rechtwinklige Dreiecke untersuchen, andererseits mithilfe von Sinussatz und Kosinussatz sogar an beliebigen Dreiecken fehlende Seiten oder Winkel berechnen.