Die Determinante ist eine Funktion, die jeder quadratischen Matrix auf zunächst etwas willkürlich scheinende, aber eindeutige Weise eine Zahl zuordnet. Das Besondere daran ist, dass man mithilfe der Determinante wichtige Informationen über die Matrix und ihre Spalten- bzw. Zeilenvektoren gewinnt.
In zwei Dimensionen, also für die „zweireihige“ Determinante einer 2×2-Matrix A, lautet die Definition:
\(\det A = \det \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \equiv \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11} a_{22} - a_{12} a_{21} \)
In drei Dimensionen, also für die „dreireihige“ Determinante einer 3×3-Matrix A, gilt
\(\det A =\det \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \equiv \begin{vmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \\ \ \\ \quad \quad \ \ = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{31}a_{22}a_{13} - a_{32}a_{23}a_{11} - a_{33}a_{21}a_{12}\)
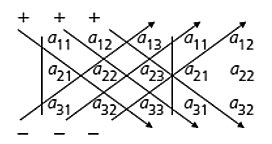
Als Merkhilfe kann man das Schema der sog. Sarrus-Regel (nach dem franz. Mathematiker P. F. Sarrus) verwenden:
Die Elemente werden längs der Pfeile miteinander multipliziert. Produkte mit schräg nach unten laufenden Pfeilen werden addiert (positives Vorzeichen, +), Pfeile, die von unten nach schräg oben zeigen, werden subtrahiert (negatives Vorzeichen, –).
Beispiel:
\(\begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{vmatrix} =1 \cdot 5 \cdot 9 + 2 \cdot 6 \cdot 7 + 3 \cdot 4 \cdot 8 - 7 \cdot 5 \cdot 3 - 8 \cdot 6 \cdot 1 - 9 \cdot 4 \cdot 2 = 0\)
Rechenregeln für Determinanten:
- Der Wert einer Determinante bleibt gleich, wenn man die Matrix transponiert, also Zeilen mit Spalten vertauscht:
det A = det AT. - Der Wert einer Determinante bleibt gleich, wenn man eine Spalte (Zeile) mit einem Faktor multipliziert und zu einer anderen Spalte (Zeile) addiert (dies macht man sich beim Lösen von linearen Gleichungssystemen zunutze).
- Wenn man eine n×n-Matrix mit einem Skalar multipliziert, muss man den Determinante mit der n-ten Potenz des Faktors multiplizieren:
det(k · A) = kn · det A. - Wenn man zwei Spalten bzw. zwei Zeilen miteinander vertauscht, ändert die Determinante ihr Vorzeichen.
- Wenn in einer Matrix alle Koeffizienten einer Spalte oder Zeile null sind, ist ihre Determinante null.
- Wenn die Spaltenvektoren oder die Zeilenvektoren linear abhängig sind, ist die Matrix ebenfalls null.