Ein Baumdiagramm ist eine übersichtliche Darstellung der möglichen Ausgänge von mehrstufigen Zufallsexperimenten. Die Bezeichnung „Baumdiagramm“ ist insofern etwas ungeschickt, als meistens die „Wurzel“ oben gezeichnet wird und das Diagramm sich dann nach unten hin verzweigt.
Im Baumdiagramm steht jede Verzweigung für eine Stufe des Experiments, also eines der zugehörigen Einzelexperimente. Am Verzweigungspunkt notiert man (wenn es nicht sowieso schon klar ist) die möglichen Ergebnisse des jeweiligen Experiments, am Ende eines Zweigs das zugehörige Ergebnis und seitlich am Zweig die Einzelwahrscheinlichkeit dieses Ergebnisses.
Wenn auf allen Stufen dasselbe Zufallsexperiment stattfindet (nur eben n-mal), also eine Bernoulli-Kette bzw. ein Urnenmodell dargestellt wird, sollte man beim Ziehen ohne Zurücklegen trotzdem an jeder Verzweigung den aktuellen Urneninhalt notieren, da dieser sich bei jeder Ziehung (auf jeder Stufe) ändert. Nur beim Ziehen mit Zurücklegen enthält die Urne auf allen Stufen dieselben Kugeln.
Den Weg vom Startpunkt eines Baumdiagramms bis zu den Ergebnissen der letzten (untersten) Stufen wird Pfad genannt. Daher kommt die Bezeichnung Pfadregeln für die beiden wichtigsten Rechenregeln beim Baumdiagramm.
Beispiel:
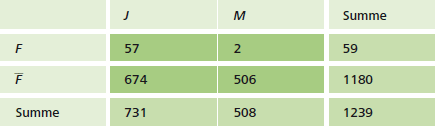
Beim Sehtest in einer Schule werden 1239 Jungen (J) und Mädchen (M) auf Rotgrünschwäche (die sog. „Farbenblindheit“, F) untersucht. Die folgende Vierfeldertafel dokumentiert die gefunden absoluten Häufigkeiten:
Wir fassen die Untersuchung jetzt als Durchführung eines zweistufigen Zufallsexperiments auf, wobei die erste Stufe der Auswahl eines Jungen oder Mädchens (Merkmal: Geschlecht) und die zweite Stufe dem eigentlichen Sehtest (Merkmal: Farbenblindheit) entspricht.
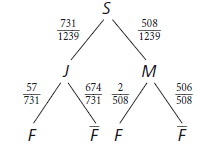
Das Baumdiagramm sieht dann so aus („S“ steht Schüler/-in):
Mit der ersten Pfadregel, der Produktregel, kann man sofort die Wahrscheinlichkeit dafür ausrechen, dass ein zufällig bestimmtes Mitglied der Schulgemeinschaft ein farbenblinder Junge ist:
\(P (J \text{ und } F) = \displaystyle\frac{731}{1 239} \cdot \frac{57}{731} \approx 4,6\,\%\)
Mit der zweiten Pfadregel, der Additionsregel, ergibt sich die Wahrscheinlichkeit dafür, dass ein zufällig bestimmtes Mitglied der Schulgemeinschaft farbenblind ist:
\(P (F) = \displaystyle \frac{731}{1 239} \cdot \frac{57}{731} + \frac{508}{1239} \cdot \frac{2}{508} \approx 4,8\,\%\)
Man kann ein Baumdiagramm auch so interpretieren, dass es die jeweiligen bedingten Wahrscheinlichkeiten anzeigt, wie die folgende Abbildung verdeutlicht:
Unten im Baumdiagramm steht also beispielsweise ganz links das Ereignis A unter der Bedingung/Voraussetzung, dass vorher B eingetreten ist, und ganz rechts Ereignis \(\bar A\) unter der Bedingung/Voraussetzung, dass vorher \(\bar B\) eingetreten ist,
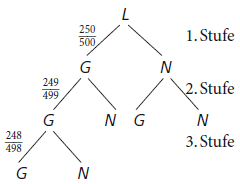
Das nächste Bild zeigt, dass es nicht immer notwendig ist, ein Baumdiagramm vollständig zu beschriften, was recht mühsam werden kann. Gefragt ist hier die Wahrscheinlichketi dafür, aus einer Lostrommel mit 500 Losen nacheinander zwei bzw. drei Gewinne zu ziehen, wenn zu Beginn 250 Gewinne in der Trommel waren und die gezogenen Lose gleich eingelöst, d. h. nicht zurückgelegt werden:
Wiederum mit der Produktregel ergibt sich: \(P (2\text{ Gewinne}) = \displaystyle \frac{250}{500} \cdot \frac{249}{499} \approx 0,249 \triangleq 24,9 %\) und \(P (3 \text{ Gewinne}) = \displaystyle \frac{250}{500} \cdot \frac{249}{499} \cdot \frac{248}{498} \approx 0,124 \triangleq 12,4 %\).