Die Arkusfunktionen („Bogenfunktionen“) sind die Umkehrfunktionen der trigonometrischen Funktionen (Winkelfunktionen). Sie geben also die Antwort auf die Frage, welcher Winkel zu einem bestimmten Wert von Sinus, Kosinus bzw. Tangens gehört.
Da man sich bei der Diskussion von Funktionen das Leben ungern mit Einheiten wie „Grad“ schwer macht, verwendet man hier in der Regel das Bogenmaß.
Da alle drei Winkelfunktionen keine eineindeutigen Funktionen sind, sondern jeder Wert innerhalb des jeweiligen Wertebereichs sogar unendlich oft auftaucht, muss man den Definitionsbereich einschränken, damit man eine sinnvolle Umkehrfunktion definieren kann. Und zwar betrachtet man nur jeweils den Abschnitt des Funktionsgraphen, der den Ursprung bzw. die Stelle x = 0 enthält. Damit haben die Funktionen Arkussinus und Arkuskosinus den Definitionsbereich D = [–1; 1] und die Arkustangensfunktion hat \(D = \mathbb R\); siehe Tabelle, wo auch die Wertebereiche angegeben sind.
| Definitionsbereich D | Wertebereich D | |
|---|---|---|
| Sinus | \(\mathbb R\) | [–1; 1] |
| Sinus (eingeschränkt) | \(\displaystyle \left[-\frac \pi 2; \ \frac \pi 2 \right]\) | [–1; 1] |
| Arkussinus | [–1; 1] | \(\displaystyle \left[-\frac \pi 2; \ \frac \pi 2 \right]\) |
| Kosinus | \(\mathbb R\) | [–1; 1] |
| Kosinus (eingeschränkt) | \(\displaystyle \left[-\pi; \ \pi \right]\) | [–1; 1] |
| Arkuskosinus | [–1; 1] | \(\displaystyle \left[-\pi; \ \pi \right]\) |
| Tangens | \(\displaystyle \mathbb R \setminus \left\{ \left. \frac{i + 1}{2}\pi \right| \ i \in \mathbb Z \right\}\) | \(\mathbb R\) |
| Tangens (eingeschränkt) | \(\displaystyle \left]-\frac \pi 2; \ \frac \pi 2 \right[\) | \(\mathbb R\) |
| Arkustangens | \(\mathbb R\) | \(\displaystyle \left]-\frac \pi 2; \ \frac \pi 2 \right[\) |
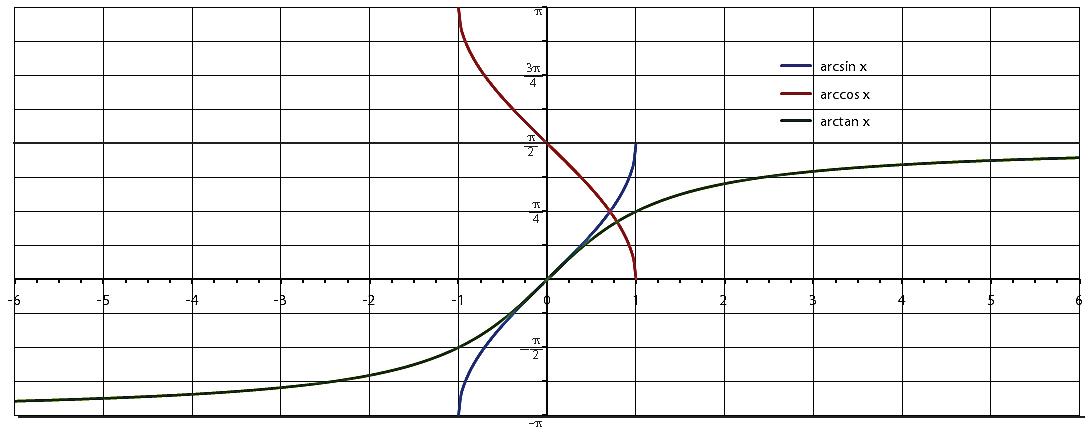
Die Abbildung zeigt die Funktionsgraphen der drei Arkusfunktionen: