Eine Zahlenfolge, bei der die Differenz d = an+1 – an von zwei aufeinanderfolgenden Gliedern für alle \(n \in \mathbb N\) gleich groß (konstant) ist, nennt man einen arithmetische Zahlenfolge.
Die Bezeichnung „arithmetische Zahlenfolge“ kommt daher, dass von drei aufeinanderfolgenden Gliedern an–1, an und an+1 das mittlere Glied an immer gleich dem arithmetischen Mittel der beiden äußeren Glieder ist: \(\displaystyle a_n = \frac{a_{n-1} + a_{n + 1}}{2}\ (n \in \mathbb{N})\).
Für arithmetische Zahlenfolgen gilt das explizite Bildungsgesetz: an = a1 + (n – 1) · d (\(n \in \mathbb{N}\)).
Beispiel:
- Die Zahlenfolge (an) = –1; 0,5; 2; 3,5; 5; … hat das explizite Bildungsgesetz an = –1 + (n – 1) · 1,5 (\(n \in \mathbb{N}\)), also d = 1,5.
Wenn die Differenz d zweier benachbarter Folgenglieder positiv ist (d > 0), nimmt die Zahlenfolge streng monoton zu, bei d = 0 ist sie konstant und für d < 0 nimmt sie streng monoton ab.
Die Punkte Pn(n|an), die den Funktionsgraphen einer arithmetischen Zahlenfolge liegen auf der Geraden mit der Gleichung y = f(x) = d · x + (a1 – d), und zwar immer bei ganzzahlig-positiven x-Werten.
Beispiele:
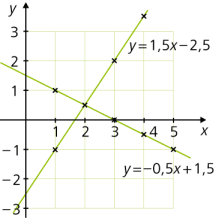
- \(a_n = - 1 + (n - 1) \cdot 1,5\): \(y = 1,5x + (- 1 - 1,5) = 1,5x -2,5\)
- \(a_n = 1 + (n - 1) \cdot (- 0,5)\): \(y = - 0,5x + (1 - (- 0,5)) = - 0,5x + 1,5\)
p>