Was du wissen musst
-
Wie kann man sich den Höhensatz und den Kathetensatz anschaulich vorstellen?
Eine anschauliche Bedeutung erhältst du, wenn du dir die Flächen am Dreieck vorstellst, die zu den einzelnen Termen aus der Definition von Höhensatz und Kathetensatz gehören.
Der Höhensatz besagt dann, dass die Fläche des Quadrates mit der Seitenlänge \(h\) gleich der Fläche des Rechtecks mit den Seitenlängen \(p\) und \(q\) ist.
\(h^2 = p\cdot q\)
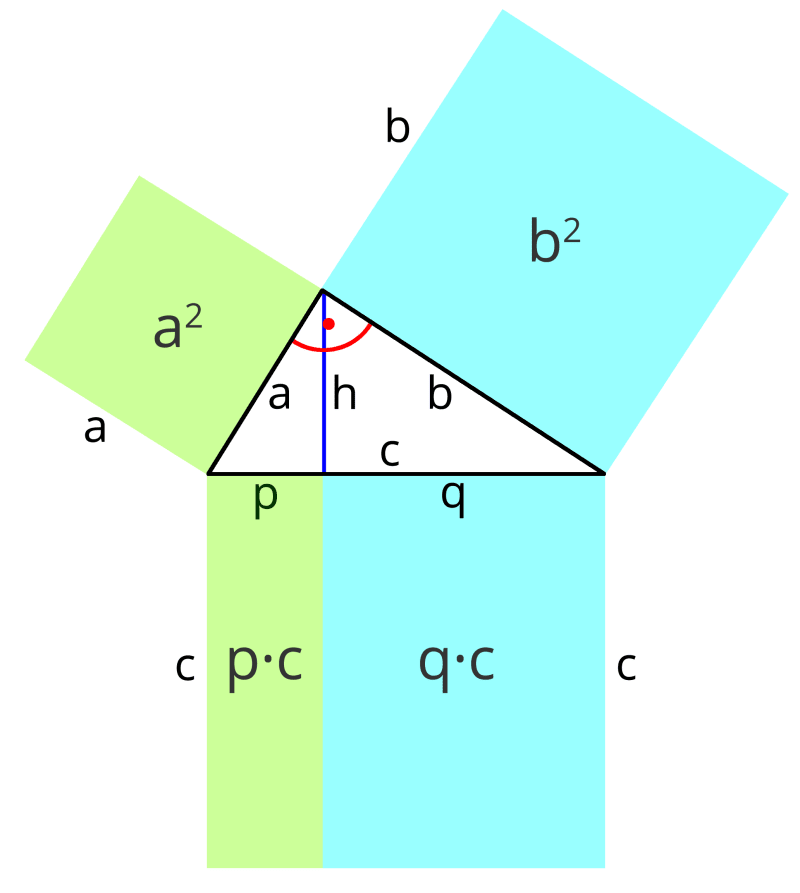
Ähnliches gilt für den Kathetensatz. Hier hat das Quadrat mit der Seitenlänge \(a\) bzw. \(b\) die gleiche Fläche wie das Rechteck mit den Seitenlängen \(p\) und \(c\) bzw. \(q\) und \(c\).
\(a^2 = p\cdot c\)
\(b^2 = q\cdot c\)
-
Wie erkennt man, ob Höhensatz oder Kathetensatz in der Aufgabe nötig sind?
Es gibt drei wichtige Anhaltspunkte dafür, dass du bei einer Aufgabe den Höhensatz oder den Kathetensatz anwenden musst.
- Die Höhe \(h\) der Hypotenuse ist gegeben oder eingezeichnet.
- Eine oder beide Längen der Strecken \(p\) und \(q\) sind gegeben.
- Der Satz des Pythagoras kann dir nicht weiterhelfen.
-
Wie beweist man den Höhensatz und den Kathetensatz?
Den Höhensatz und den Kathetensatz kannst du auf algebraischem oder auch auf geometrischem Weg beweisen.
Algebraische Beweise
Es ist möglich, den Höhensatz und den Kathetensatz aus dem Satz des Pythagoras herzuleiten. Den schreibst du einmal für das Ausgangsdreieck auf.
- \(\color{red}{a^2} + \color{green}{b^2} = \color{blue}{c^2}\)
Und dann wendest du ihn auf die inneren beiden Dreiecke an, die entstehen, wenn die Höhe \(h\) eingezeichnet wird.
- \(h^2 + p^2 = \color{red}{a^2}\)
- \(h^2 + q^2 = \color{green}{b^2}\)
Außerdem weißt du noch, dass die Seite \(c\) aus den Längen \(p\) und \(q\) besteht (\(c = p + q\)). Dadurch gilt auch:
- \((p + q)^2 = \color{blue}{c^2}\)
Nun ersetzt du \(a^2\), \(b^2\) und \(c^2\) in der ersten Gleichung mithilfe der anderen Gleichungen. Danach kannst du die Gleichung so umformen, dass sie den Höhensatz ergibt. Der Beweis für den Kathetensatz funktioniert auf die gleiche Weise. Der Unterschied ist hier nur, dass du entweder \(a^2\) oder \(b^2\) in der ersten Gleichung nicht ersetzt.
Geometrische Beweise
Am einfachsten kann man die beiden Sätze über die Ähnlichkeit von Dreiecken beweisen. Die gleichen Winkel verraten dir, dass die beiden inneren Dreiecke, die durch das Einzeichnen der Höhe \(h\) entstehen, ähnlich sind. Die daraus resultierende Bedingung für die Seitenverhältnisse liefert dir nach einer kleinen Umformung den Höhensatz.
Die beiden Formeln des Kathetensatzes erhältst du jeweils durch die Ähnlichkeit des äußeren Dreiecks mit den beiden inneren Dreiecken (ebenfalls gleiche Winkel).
-
Wozu braucht man den Höhensatz und den Kathetensatz?
Den Höhensatz und den Kathetensatz brauchst du im Matheunterricht vor allem für Geometrieaufgaben, bei denen du den Satz des Pythagoras nicht anwenden kannst, weil die dafür nötigen Seitenlängen nicht gegeben sind.
Im Alltag kannst du die beiden Sätze vor allem dann verwenden, wenn du die Höhe bei rechtwinkligen Dreiecken bestimmen möchtest. Das kann zum Beispiel der Fall sein, wenn du dich fragst, wie hoch das rechtwinklige Dach deines Haus sein wird. Den Satz des Pythagoras wirst du allerdings im Alltag wahrscheinlich öfter brauchen.