-
Aufgabe 1
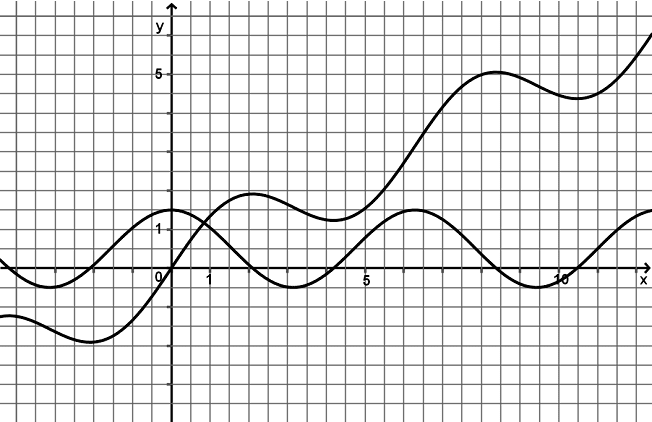
Im Material sind die Graphen einer Funktion der Funktionenschar \(f_k\) mit \(f_k(x) = \mathrm{sin}(x) + k·x,\ k \in \mathbb R\), und ihrer Ableitungsfunktion zu sehen.
1.1
Geben Sie die erste Ableitung von \(f_k \) an. Beschriften Sie die Graphen im Material jeweils mit der zugehörigen Funktion. Bestimmen Sie \(k\) für die im Material abgebildeten Funktionsgraphen.
(4 BE)
1.2
Untersuchen Sie unter Einbeziehung der Eigenschaften des Graphen der Ableitungsfunktion, für welche Werte von \(k\) die Scharfunktionen \(f_k \) Extremstellen haben.
(5 BE)
1.3
Skizzieren Sie im Material die Fläche zwischen dem Graphen von \(f_k \) und der Geraden mit der Gleichung \(y=k \cdot x\) über dem Intervall \([0;2π]\) für den in Aufgabe 1.1 bestimmten Wert von \(k\).
(2 BE)
1.4
Betrachtet werden für jede Scharfunktion \(f_k \) die Flächenstücke zwischen dem Graphen von \(f_k \) und der Geraden mit der Gleichung \(y=k \cdot x\), die jeweils von zwei aufeinanderfolgenden Schnittpunkten begrenzt werden. Zeigen Sie mithilfe geeigneter Rechnungen, dass alle diese Flächenstücke unabhängig von \(k\) gleich groß sind.
(5 BE)
Graphen einer Funktion der Funktionenschar \(f_k\) mit \(f_k(x)=sin(x)+k\cdot x, \ k\in\mathbb R\) und ihrer Ableitungsfunktion.